1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-
1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-
Ak si nevieš poradiť s niektorou z úloh, pozri sipár tipov.
1. ÚLOHA
Poarot hľadal všetky štvorciferné čísla končiace číslicou také, že sú deliteľné všetkými svojimi číslicami. Pomôžte mu ich nájsť a dokážte, že iné neexistujú.
Pozn.: Nulou sa deliť nedá.
2. ÚLOHA
Herkules a Poarot hrajú hru na šachovnici , Herkules s bielymi a Poarot s čiernymi kameňmi. Každý hráč má kameňov. Herkules začína – umiestni jeden kameň na jedno z voľných polí šachovnice. Striedajú sa s Poarotom po jednom kameni. Nakoniec, keď sa zbavia všetkých svojich kameňov, dostane Herkules bod za každý riadok a každý stĺpec, v ktorom majú prevahu biele kamene, Poarot dostane bod za každý riadok a každý stĺpec s prevahou čiernych kameňov. Pokiaľ má Herkules viac bodov, víťazí, ak nie, vyhráva Poarot. Ktorý z hráčov má víťaznú stratégiu? Víťazná stratégia je postup, podľa ktorého keď jeden hráč hrá, tak vyhrá bez ohľadu na ťahy súpera.
3. ÚLOHA
Herkules písal svoj trojciferný PIN od trezora na klávesnici, kde sú v prvom riadku čísla od do , v druhom od do a v treťom od do .
Poarot mu otočil klávesnicu o (teda prvý riadok je ), a keď klikal na miesta, na ktoré by klikal pri zadávaní svojho pôvodného PINu, napísal číslo, ktoré bolo celočíselným násobkom pôvodného PINu.
Aké všetky PINy mohol mať Herkulov trezor?
4. ÚLOHA
Herkules a Poarot majú šachovnicu veľkosti . Šerlok je figúrka, ktorá môže preskakovať iné figúrky a v jednom ťahu sa posunie vodorovne o párny počet polí alebo zvislo o nepárny počet polí. Inú figúrku vybije, ak skočí na pole, na ktorom daná figúrka stojí. Koľko najviac Šerlokov vieme umiestniť na šachovnicu tak, aby sa žiadni dvaja neohrozovali?
5. ÚLOHA
Poarot kúpil koberec tvaru štvorca na obrázku, ktorého vzor tvorí 21 menších štvorcov. Dĺžky strán dvoch z nich sú vpísané v obrázku. Aká je dĺžka strany koberca?
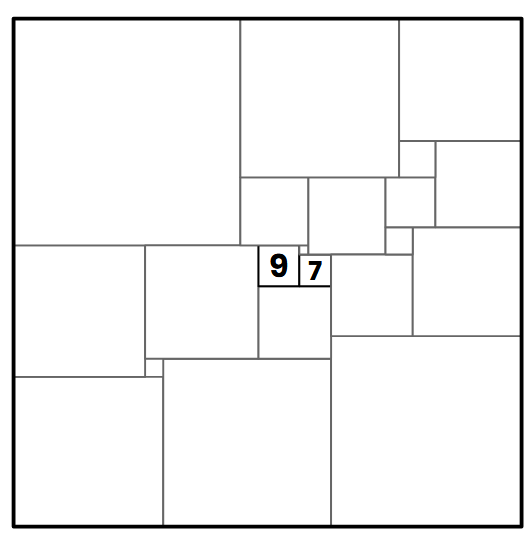
6. ÚLOHA
Kachlička v Herkulovej kúpeľni má tvar štvorca . Na strane leží bod a na strane bod tak, že úsečky a sú rovnako dlhé. Bod je päta kolmice z bodu na priamku .
Dokážte, že uhol je pravý.


