1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-
1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-1. séria-Termín: 16. 03. 2026 19:00-Prebieha opravovanie-
Ak si nevieš poradiť s niektorou z úloh, pozri sipár tipov.
1. ÚLOHA
Traja pomocníci majú dokopy skrutiek, pričom každý ich má toľko, koľko má rokov. Najmladší navrhne takúto výmenu: „Najprv si ja nechám polovicu svojich skrutiek a zvyšné rozdelím rovnakým dielom zvyšným dvom. Potom to isté urobí prostredný pomocník, následne to isté urobí najstarší pomocník.“ Po výmene zistia,
že majú navzájom rovnaké počty skrutiek. Koľko rokov majú jednotliví pomocníci?
2. ÚLOHA
Na vrchnom kryte stroja času je v kruhu náhodne rozmiestnených niekoľko čísel od do nejakého čísla, každé práve raz. Platí, že žiadne dve susedné čísla nie sú párne, žiadne dve susedné čísla nie sú nepárne a žiadne dve susedné čísla nemajú rozdiel . Koľko najmenej môže byť čísel v kruhu? Prečo to pre menej čísel nie je možné?
3. ÚLOHA
Finálny trik kúzelníka Ľuba spočíva v tom, že vždy poprosí niekoho v publiku, aby mu napísal na papier hocikoľko kladných celých čísel. Ľubo tvrdí, že si potom z nich vždy dokáže vybrať trojicu čísel, ktorých súčet je deliteľný tromi. Pri akom najmenšom počte čísel si Ľubo môže byť istý, že to dokáže?
4. ÚLOHA
Alexander a Barbora hrajú hru, kde na papieri majú napísané čísla od po , každé práve raz. Hráči sa striedajú a vždy si počas svojho ťahu vyberú dve čísla, ktoré zmažú, odčítajú menšie od väčšieho a výsledok napíšu na papier (ak sú čísla rovnaké, nové číslo je ). Ak posledné číslo napísané na papieri je párne, vyhrá Alexander, ale ak je nepárne, vyhrá Barbora.
a) Kto vyhrá, ak začína Alexander?
b) Kto vyhrá, ak začína Barbora?
5. ÚLOHA
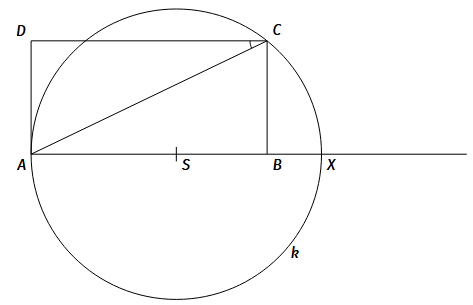
V knihe sa píše, že symbol je v tvare obdĺžnika , v ktorom uhol má veľkosť stupňov. Na strane vo vzdialenosti od bodu sa nachádza bod , ktorý je stredom kružnice , na ktorej ležia body aj . Ak predĺžime úsečku , pretne druhýkrát kružnicu v bode . Nájdite veľkosť úsečky . Úlohu neriešte meraním ani rysovaním.
6. ÚLOHA
Alexander má vo svojich dvoch vreckách niekoľko cukríkov, pričom v každom má aspoň , no menej ako . Kráľovná vidí, že v pravom vrecku má viac cukríkov ako v ľavom. Kráľovná si môže vždy tipnúť buď koľko cukríkov má Alexander vo vreckách dokopy, alebo aký je rozdiel počtu cukríkov v pravom a v ľavom vrecku. Alexander jej nechce klamať, tak vždy pravdivo odpovie áno alebo nie na jej tip. Koľko najmenej tipov bude kráľovnej stačiť na to, aby zistila koľko cukríkov má Alexander v ktorom vrecku bez ohľadu na to, koľko ich tam má?


