
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára STROM, 32. ročník - Letný semester
Vzorové riešenia 1. série nájdeš v časopise STROM-32-5
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Termín série: 6. marec 2008 0:00:00
1. V poslednej dobe nadobudol veľkú popularitu japonský hlavolam SUDOKU.
Klasické sudoku je tabuľka veľkosti $9\times 9$ rozdelená na 9 štvorcov veľkosti $3\times 3$,
pričom v niektorých políčkach tabuľky sú vpísané čísla od 1 po 9. Takúto tabuľku nazvime zadanie.
Úlohou je doplniť do všetkých ostatných políčok čísla od 1 po 9 tak, aby v každom stĺpci, riadku, štvorci
$3\times 3$ bolo každé číslo práve raz. Takto vyplnenú tabuľku nazvime riešením daného zadania.
Uvažujme menšie a jednoduchšie sudoku: Tabuľku veľkosti $4\times 4$ rozdelenú na 4 štvorce veľkosti $2\times 2$ chceme vyplni číslami od 1 po 4 tak, aby v každom riadku, každom ståpci, každom štvorci $2\times 2$ bolo každé èíslo práve raz.
a) Koľko existuje všetkých možných riešení takéhoto sudoku $4\times 4$?
b) Nájdite také zadanie sudoku veľkosti $4\times 4$, v ktorom sú vpísané len 4 čísla, a pritom má jediné riešenie.
c) Dokážte, že ak zadanie sudoku $4\times 4$ má jediné riešenie, tak sú v òom už vpísané aspoň 4 čísla (alebo ekvivalentne: dokážte, že ak sú zadané najviac tri čísla, tak také sudoku buď nemá riešenie, alebo má viac ako jedno riešenie).
Uvažujme menšie a jednoduchšie sudoku: Tabuľku veľkosti $4\times 4$ rozdelenú na 4 štvorce veľkosti $2\times 2$ chceme vyplni číslami od 1 po 4 tak, aby v každom riadku, každom ståpci, každom štvorci $2\times 2$ bolo každé èíslo práve raz.
a) Koľko existuje všetkých možných riešení takéhoto sudoku $4\times 4$?
b) Nájdite také zadanie sudoku veľkosti $4\times 4$, v ktorom sú vpísané len 4 čísla, a pritom má jediné riešenie.
c) Dokážte, že ak zadanie sudoku $4\times 4$ má jediné riešenie, tak sú v òom už vpísané aspoň 4 čísla (alebo ekvivalentne: dokážte, že ak sú zadané najviac tri čísla, tak také sudoku buď nemá riešenie, alebo má viac ako jedno riešenie).
2. Jožko si raz dlhú chvíľu v škole krátil tým, že sa snažil vyplni tabuľku $5 \times 5$ štvorčekov
útvarmi z obrázku, (pričom ich mohol ľubovoľne otočiť alebo prevrátiť, nesmeli sa však prekrývať)
Okamžite prišiel na to, že sa mu minimálne 1 políčko musí zvýši. Nie vždy to však bolo to isté políčko. Viete Jožkovi povedať,
ktoré políčka to môžu by?
b) Ferko si všimol Jožkovu zábavku a hneď ju začal riešiť. Keďže sa mu Jožkova úloha zdala príliš ľahká, tak on si zobral ľubovoľnú tabuľku $n \times n$ štvorčekov. Koľko políčok sa najmenej Ferkovi zvýši? Ktoré políčka to môžu byť?
Svoje tvrdenia nezabudnite poriadne zdôvodniť.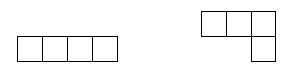
b) Ferko si všimol Jožkovu zábavku a hneď ju začal riešiť. Keďže sa mu Jožkova úloha zdala príliš ľahká, tak on si zobral ľubovoľnú tabuľku $n \times n$ štvorčekov. Koľko políčok sa najmenej Ferkovi zvýši? Ktoré políčka to môžu byť?
Svoje tvrdenia nezabudnite poriadne zdôvodniť.

3. a) Paľko si do zošita píše postupnosti čísel. Začne celým číslom 0, a potom k nemu pripočíta nejaké prirodzené číslo $a$. Potom znova
pripočíta $a$, a znova, a znova. Paľkova postupnos teda vyzerá takto: $0, a, 2a, 3a, 4a,\dots$
Jožko si zvolil prirodzené číslo $b$ a do zošita si začal písa zvyšky Paľkových čísel po delení číslom $b$ (presne v tom istom poradí, v akom mal napísané èísla Paľko). Ukážte, že bez ohľadu na to, aké čísla si chlapci zvolia, bude od istého miesta Jožkova postupnosť obsahovať presne tie isté čísla, ako na začiatku (teda je periodická).
b) Aj Samko si začal písať do zošita čísla, ale namiesto sčítania nasobí a namiesto nuly začína jednotkou. Takže jeho postupnosť vyzerá takto: $1, a, a^2, a^3, \dots$
Mirko si myslí, že keï si zvolí hocijaké prirodzené číslo $b$, začnú sa zvyšky Samkových čísel po delení číslom $b$ tiež od istého miesta opakovať. Má Mirko pravdu?
c) Pani uciteľka si všimla hru chlapcov, a povedala: "Nech $P(x)$ je lubovoľný polynóm s celočíselnými koeficientami. Vytvorme postupnosť čísel $$ P(1)^1, P(2)^2,\dots,P(n)^n,\dots $$ Čo viete o takejto postupnosti povedať?" Dežko si hneď všimol, že nech si zvolí hocijaké prirodzené číslo $b$, zvyšky jednotlivých členov tejto postupnosti po delení číslom $b$ tvoria periodickú postupnosť. Dokážte, že Dežko má pravdu.
Jožko si zvolil prirodzené číslo $b$ a do zošita si začal písa zvyšky Paľkových čísel po delení číslom $b$ (presne v tom istom poradí, v akom mal napísané èísla Paľko). Ukážte, že bez ohľadu na to, aké čísla si chlapci zvolia, bude od istého miesta Jožkova postupnosť obsahovať presne tie isté čísla, ako na začiatku (teda je periodická).
b) Aj Samko si začal písať do zošita čísla, ale namiesto sčítania nasobí a namiesto nuly začína jednotkou. Takže jeho postupnosť vyzerá takto: $1, a, a^2, a^3, \dots$
Mirko si myslí, že keï si zvolí hocijaké prirodzené číslo $b$, začnú sa zvyšky Samkových čísel po delení číslom $b$ tiež od istého miesta opakovať. Má Mirko pravdu?
c) Pani uciteľka si všimla hru chlapcov, a povedala: "Nech $P(x)$ je lubovoľný polynóm s celočíselnými koeficientami. Vytvorme postupnosť čísel $$ P(1)^1, P(2)^2,\dots,P(n)^n,\dots $$ Čo viete o takejto postupnosti povedať?" Dežko si hneď všimol, že nech si zvolí hocijaké prirodzené číslo $b$, zvyšky jednotlivých členov tejto postupnosti po delení číslom $b$ tvoria periodickú postupnosť. Dokážte, že Dežko má pravdu.
4. Nech $ABC$ je ostrouhlý trojuholník s priesečníkom výšok $V$.
a) Označme $V_a$, $V_b$, $V_c$ po poradí obrazy priesečníka výšok v osových súmernostiach podľa strán $BC$, $CA$, $AB$. Dokážte, že body $V_a$, $V_b$, $V_c$ ležia na kružnici opísanej trojuholníku $ABC$.
b) Označme $U_a$, $U_b$, $U_c$ po poradí obrazy priesečníka výšok v stredových súmernostiach podľa stredov strán $BC$, $CA$, $AB$. Dokážte, že body $U_a$, $U_b$, $U_c$ ležia na kružnici, ktorej polomer je rovnaký ako polomer kružnice opísanej trojuholníku $ABC$.
c) Označme $U_a$, $U_b$, $U_c$ po poradí obrazy priesečníka výšok v stredových súmernostiach podľa stredov strán $BC$, $CA$, $AB$. Dokážte, že trojuholníky $U_aU_bU_c$ a $ABC$ sú zhodné.
a) Označme $V_a$, $V_b$, $V_c$ po poradí obrazy priesečníka výšok v osových súmernostiach podľa strán $BC$, $CA$, $AB$. Dokážte, že body $V_a$, $V_b$, $V_c$ ležia na kružnici opísanej trojuholníku $ABC$.
b) Označme $U_a$, $U_b$, $U_c$ po poradí obrazy priesečníka výšok v stredových súmernostiach podľa stredov strán $BC$, $CA$, $AB$. Dokážte, že body $U_a$, $U_b$, $U_c$ ležia na kružnici, ktorej polomer je rovnaký ako polomer kružnice opísanej trojuholníku $ABC$.
c) Označme $U_a$, $U_b$, $U_c$ po poradí obrazy priesečníka výšok v stredových súmernostiach podľa stredov strán $BC$, $CA$, $AB$. Dokážte, že trojuholníky $U_aU_bU_c$ a $ABC$ sú zhodné.
Vzorové riešenia 1. série nájdeš v časopise STROM-32-5
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Termín série: 21. apríl 2008 0:00:00
1. Dada dostala v Nórsku úžasnú kalkulačku. Ak zadáte prirodzené èíslo $n$ a stlačíte tlačidlo
označené symbolom $\ast$, v kalkulačke to zarachotí a na displeji sa objaví prirodzené èíslo,
nazvime ho $n^\ast$. Dada s pomocou slovníka a návodu na použitie kalkulačky zistila, že s číslom $n$
sa deje toto:
Prirodzené číslo $n$ sa prevedie do dvojkovej sustavy. Počet jednotiek a počet núl (za prvou jednotkou) v získanom čísle sa zväčší o jedna. Získané dve čísla sa spolu vynásobia, výsledný súčin sa objaví na displeji. Napríklad 13 ($8+4+1$) v dvojkovej sústave je $1101$, takže $13^\ast$ je $(3+1)(1+1)$ čiže 8. Keď zadáme $8 = 1000_2$, kalkulačka vyráta $8^\ast=(1+1)(3+1)$, čiže opäť 8.
a) Zistite $2008^\ast$.
b) Zistite, pre koľko prirodzených čísel $n$ (vrátane 2008) platí $n^\ast=2008^\ast$.
c) Zistite, pre koľko prirodzených čísel $n$ platí $n^\ast=n$. Ktoré sú to čísla?
Prirodzené číslo $n$ sa prevedie do dvojkovej sustavy. Počet jednotiek a počet núl (za prvou jednotkou) v získanom čísle sa zväčší o jedna. Získané dve čísla sa spolu vynásobia, výsledný súčin sa objaví na displeji. Napríklad 13 ($8+4+1$) v dvojkovej sústave je $1101$, takže $13^\ast$ je $(3+1)(1+1)$ čiže 8. Keď zadáme $8 = 1000_2$, kalkulačka vyráta $8^\ast=(1+1)(3+1)$, čiže opäť 8.
a) Zistite $2008^\ast$.
b) Zistite, pre koľko prirodzených čísel $n$ (vrátane 2008) platí $n^\ast=2008^\ast$.
c) Zistite, pre koľko prirodzených čísel $n$ platí $n^\ast=n$. Ktoré sú to čísla?
2. Majme trojuholník $ABC$. Nech $P$ je priesečník osi uhla $BAC$ a osi strany $BC$.
Ďalej nech body $K$, $L$, $M$ sú postupne päty kolmíc z bodu $P$ na priamky $AB$, $BC$, $CA$. Dokážte, že
a) trojuholníky $PKB$ a $PMC$ sú podobné,
b) štvoruholník $ABPC$ je tetivový,
c) body $K$, $L$, $M$ sú kolineárne.
a) trojuholníky $PKB$ a $PMC$ sú podobné,
b) štvoruholník $ABPC$ je tetivový,
c) body $K$, $L$, $M$ sú kolineárne.
3. Fibonacciho postupnosť $(F_n)$ je definovaná vzťahom $F_{n+2}=F_{n+1}+F_n$ pre $n\ge 1$ a počiatočnými hodnotami $F_1 = 1$,
$F_2 = 1$.
a) Dokážte, že existuje Fibonacciho číslo deliteľné číslom 2008.
b) Existuje aritmetická postupnosť, ktorá neobsahuje žiadne Fibonacciho číslo?
a) Dokážte, že existuje Fibonacciho číslo deliteľné číslom 2008.
b) Existuje aritmetická postupnosť, ktorá neobsahuje žiadne Fibonacciho číslo?
4. Daný je ostrouhlý trojuholník $ABC$ s priesečníkom výšok $V$.
a) Dokážte, že kružnice opísané trojuholníkom $ABV$, $BCV$, $CAV$ sú zhodné.
b) V rovine sú dane tri zhodné kružnice prechádzajúce bodom $H$. Označme priesečníky dvojíc týchto kružníc $A$, $B$, $C$ (tieto body su rôzne od bodu $H$). Dokážte, že bod $H$ je ortocentrom trojuholníka $ABC$.
c) Daná je kružnica $k$ a jej tetiva $AB$. Po jednom z oblúkov tejto kružnice sa pohybuje bod $C$ rôzny od bodov $A$ a $B$. Po akej dráhe sa pohybuje priesečník výšok trojuholníka $ABC$?
a) Dokážte, že kružnice opísané trojuholníkom $ABV$, $BCV$, $CAV$ sú zhodné.
b) V rovine sú dane tri zhodné kružnice prechádzajúce bodom $H$. Označme priesečníky dvojíc týchto kružníc $A$, $B$, $C$ (tieto body su rôzne od bodu $H$). Dokážte, že bod $H$ je ortocentrom trojuholníka $ABC$.
c) Daná je kružnica $k$ a jej tetiva $AB$. Po jednom z oblúkov tejto kružnice sa pohybuje bod $C$ rôzny od bodov $A$ a $B$. Po akej dráhe sa pohybuje priesečník výšok trojuholníka $ABC$?
Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...